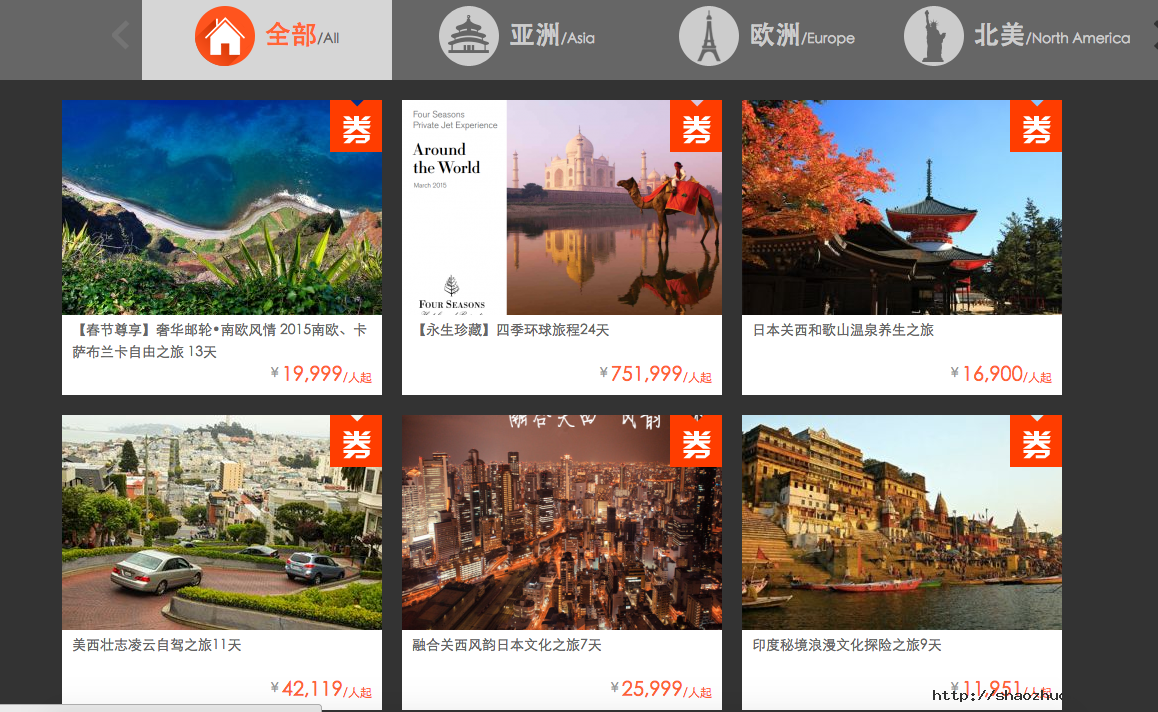
资源平台化、O2O获客以及移动端C2C服务做定制旅游
根据去年 5 月的一份《2014中国高净值人群心灵投资白皮书》,我们可以看到越来越多的有钱人热衷于在旅游领域的投资,而且相比于大众化的旅游产品,他们更青睐定制游、主题游等个性化的产品。
目前在高端旅游市场,也已兴起了一大批定制旅游品牌,比如中青旅的耀悦,众信旅游的奇迹旅行,携程的鸿鹄逸游、太美,还有兰卡之星、主打私人健康旅行的优翔、遨乐网、帝国假日等,不过中端定制市场的选手貌似并不多,目前有无二之旅、十方旅行等,另外还有将在中高端市场掘金的游心旅行。
在游心旅行的创始人蒋松涛看来,定制旅游市场是没有巨头天花板的,而且目前太美、鸿鹄逸游等高端定制逐渐趋于标准化,并不能满足人们日益多元化的需求,再者,目前并没有同时涵盖中高端市场的定制旅游品牌,游心旅行就是想填补这个空白,为这些用户提供定制、半定制旅游产品及服务,并且以平台化资源、O2O模式获取顾客,以及打造移动端C2C服务来完善整个定制体系。
资源平台化——以自营产品为主,商家资源为辅
游心旅行会经营主要出境游业务,包括定制旅游,以及自助游中消费频次较高的目的地产品,海岛、美国、澳大利亚、新西兰等地都会主力经营,然后引进一些其他的商家,像鸿鹄逸游等高端定制的资源,游心旅行也都能获取,而至于邮轮等比较低频的产品,游心旅行就不会自己去做。
之所以将资源平台化,蒋松涛表示:一则是因为旅游的消费频次低,所以通过平台引入其他供应商可以从产品类型上进行扩张,让用户有更多选择;其次是为了把控资源和用户双方,举个栗子,像赞那度虽有调性、品位,虽然产品做得很精致,事实上它也只是一个媒介,资源并不在赞那度手中,而游心旅行通过轻重取舍则能很好的把握优质资源,并保留住忠诚用户。
开设线下体验店,以O2O的模式获取顾客
一直以来,定制都是一个重线下运作的过程,即便在互联网的冲击之下,这些单价较高、消费频次低的产品也并没能有效走到线上。所以,游心旅行也采取 O2O 的模式,通过开设线下实体店来获取用户,一方面能给用户舒适的交流环境,另一方面也增加了用户对游心旅行的信任感。
打造贴身旅行管家Mr.U,在移动端提供C2C服务
用户在目的地的体验才是真正的消费环节,因此,游心旅行在移动端提供 C2C 服务来解决用户行中问题,目前姑且称它为“游心旅行管家”。
与上述的资源平台化思路,提供目的地服务的旅行管家一部分来自游心旅行全职的旅游产品经理,也会逐渐让众信、中青旅等旅游机构的专业人士入驻;另一部分则由旅行达人组成,比如即将合作的眭澔平(具体介绍见全文末尾)。
通过这种方式,既不会让游心旅行的业务模式过重,也能保证行中服务的快速有效。当用户在行程中遇突发情况,比如临时更改行程,直接就可以通过 App 联系到旅行管家,问题不大的情况下旅行达人就能直接提供建议,如果比较复杂,那么专业人士就会帮助落实这些服务。
最后,用户还能对这些旅行管家评分,优胜劣汰之下能将有潜质的旅行管家挖掘出来,而那些起初以兼职身份存在的人也可能因为挣到钱而转作全职。
而提及未来,游心旅行不仅想做一个中高端定制旅游的服务平台,他们更希望能打造出一个中高端的品牌形象,将通过定制旅游获取到的具备极强消费力的中高端用户往其他服务进行导流,比如推出Ms.U品牌——可以提供针对女士美妆、购物、养生的产品,或者是Baby.U这样的形象来为孩子推出游学等服务。
团队情况上,游心旅行团队聚集了来自鸿鹄逸游、太美旅行、穷游网、赞那度等的成员,也吸纳了腾讯、网易等互联网人士加入。蒋松涛告诉36氪,游心旅行于 2014 年 5 月份上线,上线的当月便获得了天使投资,又于 2014 年 8 月又完成了鼎晖投资与北极光邓锋的 Pre-A 轮融资,12 月份完成千万美金级别的 A 轮融资后,又并购了转型旅游定制的五星汇。
注:报道所涉融资金额由对象公司提供保证,36氪不作任何形式背书。
注:眭澔平,台湾人,集记者、作家、歌手与主持人的身份于一身,更是一名虔诚的旅行者。他是三毛的忘年交,也为实现对三毛的承诺,二十多年已走遍180多个国家,踏遍世界的每一个角落。在《我看到的世界和你们不一样》一书中,他在南极给企鹅唱着月亮代表我的心,在菲律宾古毒体验耶稣之苦,遭受钢钉穿手的洗礼......读了他的故事之后,希望你也能“与年少初始纯真的自我相逢”。
北京市小汽车摇号程序的反编译、算法及存在的问题浅析-不重复随机数列生成算法
给定一个正整数n,需要输出一个长度为n的数组,数组元素是随机数,范围为0 – n-1,且元素不能重复。比如 n = 3 时,需要获取一个长度为3的数组,元素范围为0-2,
比如 0,2,1。
这个问题的通常解决方案就是设计一个 hashtable ,然后循环获取随机数,再到 hashtable 中找,如果hashtable 中没有这个数,则输出。下面给出这种算法的代码
public static int[] GetRandomSequence0(int total)
{
int[] hashtable = new int[total];
int[] output = new int[total];
Random random = new Random();
for (int i = 0; i < total; i++)
{
int num = random.Next(0, total);
while (hashtable[num] > 0)
{
num = random.Next(0, total);
}
output[i] = num;
hashtable[num] = 1;
}
return output;
}
代码很简单,从 0 到 total - 1 循环获取随机数,再去hashtable 中尝试匹配,如果这个数在hashtable中不存在,则输出,并把这个数在hashtable 中置1,否则循环尝试获取随机数,直到找到一个不在hashtable 中的数为止。这个算法的问题在于需要不断尝试获取随机数,在hashtable 接近满时,这个尝试失败的概率会越来越高。
那么有没有什么算法,不需要这样反复尝试吗?答案是肯定的。
如上图所示,我们设计一个顺序的数组,假设n = 4
第一轮,我们取 0 – 3 之间的随机数,假设为2,这时,我们把数组位置为2的数取出来输出,并把这个数从数组中删除,这时这个数组变成了
第二轮,我们再取 0-2 之间的随机数,假设为1,并把这个位置的数输出,同时把这个数从数组删除,以此类推,直到这个数组的长度为0。这时我们就可以得到一个随机的不重复的序列。
这个算法的好处是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试。算法代码如下:
public static int[] GetRandomSequence1(int total)
{
List<int> input = new List<int>();
for (int i = 0; i < total; i++)
{
input.Add(i);
}
List<int> output = new List<int>();
Random random = new Random();
int end = total;
for (int i = 0; i < total; i++)
{
int num = random.Next(0, end);
output.Add(input[num]);
input.RemoveAt(num);
end--;
}
return output.ToArray();
}
这个算法把两个循环改成了一个循环,算法复杂度大大降低了,按说速度应该比第一个算法要快才对,然而现实往往超出我们的想象,当total = 100000 时,测试下来,第一个算法用时 44ms, 第二个用时 1038 ms ,慢了很多!这是为什么呢?问题的关键就在这个 input.RemoveAt 上了,我们知道如果要删除一个数组元素,我们需要把这个数组元素后面的所有元素都向前移动1,这个移动操作是非常耗时的,这个算法慢就慢在这里。到这里,可能有人要说了,那我们不用数组,用链表,那删除不就很快了吗?没错,链表是能解决删除元素的效率问题,但查找的速度又大大降低了,无法像数组那样根据数组元素下标直接定位到元素。所以用链表也是不行的。到这里似乎我们已经走到了死胡同,难道我们只能用hashtable 反复尝试来做吗?在看下面内容之前,请各位读者先思考5分钟。
…… 思考5分钟
算法就像一层窗户纸,隔着窗户纸,你永远无法知道里面是什么,一旦捅穿,又觉得非常简单。这个算法对于我,只用了2分钟时间想出来,因为我经常实现算法,脑子里有一些模式,如果你的大脑还没有完成这种经验的积累,也许你要花比我长很多的时间来考虑这个问题,也许永远也找不到捅穿它的方法。不过不要紧,我把这个方法公布出来,有了这个方法,你只需轻轻一动,一个完全不同的世界便出现在你的眼前。原来就这么简单……。
还是上面那个例子,假设 n = 4
第一轮,我们随机获得2时,我们不将 2 从数组中移除,而是将数组的最后一个元素移动到2的位置
这时数组变成了
第二轮我们对 0-2 取随机数,这时数组可用的最后一个元素位置已经变成了2,而不是3。假设这时取到随机数为1
我们再把下标为2 的元素移动到下标1,这时数组变成了
以此类推,直到取出n个元素为止。
这个算法的优点是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试,也不用像上一个算法那样删除数组元素,要做的只是每次把数组有效位置的最后一个元素移动到当前位置就可以了,这样算法的复杂度就降低为 O(n) ,速度大大提高。
经测试,在 n= 100000 时,这个算法的用时仅为7ms。
下面给出这个算法的实现代码
/// <summary>
/// Designed by eaglet
/// </summary>
/// <param name="total"></param>
/// <returns></returns>
public static int[] GetRandomSequence2(int total)
{
int[] sequence = new int[total];
int[] output = new int[total];
for (int i = 0; i < total; i++)
{
sequence[i] = i;
}
Random random = new Random();
int end = total - 1;
for (int i = 0; i < total; i++)
{
int num = random.Next(0, end + 1);
output[i] = sequence[num];
sequence[num] = sequence[end];
end--;
}
return output;
}
下面是n 等于1万,10万和100万时的测试数据,时间单位为毫秒。从测试数据看GetRandomSequence2的用时和n基本成正比,线性增长的,这个和理论上的算法复杂度O(n)也是一致的,另外两个算法则随着n的增大,用时超过了线性增长。在1百万时,我的算法比用hashtable的算法要快10倍以上。
| 10000 | 100000 | 1000000 | |
| GetRandomSequence0 | 5 | 44 | 1075 |
| GetRandomSequence1 | 11 | 1038 | 124205 |
| GetRandomSequence2 | 1 | 7 | 82 |
现在摇号的程序及数据都可以在官网中查看,目的就是通过信息的透明度来堵住那些说摇号系统有猫腻之类的传言,我做为一个程序员,下意识的就想看看到底是否有猫腻。
通过下载程序,导入数据,将种子数写入后,的确没有什么猫腻,但还是不死心,想研究一下算法,结果发现了惊人的事情。
此算法使用的是伪随机,简单点将就是当种子数一定,摇号数据一定,每次随机结果都是一样的。举个例子,借用某申请编码2245102443992,摇号基数序号500015,取种子数范围在100000至120000之间能中签的种子数,结果显示共132个种子数,其概率为0.66%。随机找了一个种子数100575进行计算,得出结果在左侧表中,查询2245102443992是否中签,结果显示中签,在第15916行摇中;所以大家都应该知道怎么回事了吧,只要摇号池数据确定,查询出摇号基数序号,就能算出中签的种子数都有哪些,所以公布的数据和程序又有何用?关键在于种子数的确定。