关于对称加密算法与非对称加密算法
我们来讲解下关于各种加解密算法的比较,其中有对称加密算法,非对称加密算法,散列算法等等。
对称加密算法
对称加密算法用来对敏感数据等信息进行加密,常用的算法包括:
DES(Data Encryption Standard):数据加密标准,速度较快,适用于加密大量数据的场合。
3DES(Triple DES):是基于DES,对一块数据用三个不同的密钥进行三次加密,强度更高。
AES(Advanced Encryption Standard):高级加密标准,是下一代的加密算法标准,速度快,安全级别高;
AES与3DES的比较
| 算法名称 | 算法类型 | 密钥长度 | 速度 | 解密时间(建设机器每秒尝试255个密钥) | 资源消耗 |
| AES | 对称block密码 | 128、192、256位 | 高 | 1490000亿年 | 低 |
| 3DES | 对称feistel密码 | 112位或168位 | 低 | 46亿年 | 中 |
RSA:由 RSA 公司发明,是一个支持变长密钥的公共密钥算法,需要加密的文件块的长度也是可变的;
DSA(Digital Signature Algorithm):数字签名算法,是一种标准的 DSS(数字签名标准);
ECC(Elliptic Curves Cryptography):椭圆曲线密码编码学。
ECC和RSA相比,在许多方面都有对绝对的优势,主要体现在以下方面:
抗攻击性强。相同的密钥长度,其抗攻击性要强很多倍。
计算量小,处理速度快。ECC总的速度比RSA、DSA要快得多。
存储空间占用小。ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多,意味着它所占的存贮空间要小得多。这对于加密算法在IC卡上的应用具有特别重要的意义。
带宽要求低。当对长消息进行加解密时,三类密码系统有相同的带宽要求,但应用于短消息时ECC带宽要求却低得多。带宽要求低使ECC在无线网络领域具有广泛的应用前景。
下面两张表示是RSA和ECC的安全性和速度的比较。
| 攻破时间(MIPS年) | RSA/DSA(密钥长度) | ECC密钥长度 | RSA/ECC密钥长度比 |
| 104 | 512 | 106 | 5:1 |
| 108 | 768 | 132 | 6:1 |
| 1011 | 1024 | 160 | 7:1 |
| 1020 | 2048 | 210 | 10:1 |
| 1078 | 21000 | 600 | 35:1 |
| 攻破时间(MIPS年) | RSA/DSA(密钥长度) | ECC密钥长度 | RSA/ECC密钥长度比 |
| 104 | 512 | 106 | 5:1 |
| 108 | 768 | 132 | 6:1 |
| 1011 | 1024 | 160 | 7:1 |
| 1020 | 2048 | 210 | 10:1 |
| 1078 | 21000 | 600 | 35:1 |
RSA和ECC安全模长得比较
| 功能 | Security Builder 1.2 | BSAFE 3.0 |
| 163位ECC(ms) | 1,023位RSA(ms) | |
| 密钥对生成 | 3.8 | 4,708.3 |
| 签名 | 2.1(ECNRA) | 228.4 |
| 3.0(ECDSA) | ||
| 认证 | 9.9(ECNRA) | 12.7 |
| 10.7(ECDSA) | ||
| Diffie—Hellman密钥交换 | 7.3 | 1,654.0 |
RSA和ECC速度比较
散列是信息的提炼,通常其长度要比信息小得多,且为一个固定长度。加密性强的散列一定是不可逆的,这就意味着通过散列结果,无法推出任何部分的原始信息。任何输入信息的变化,哪怕仅一位,都将导致散列结果的明显变化,这称之为雪崩效应。散列还应该是防冲突的,即找不出具有相同散列结果的两条信息。具有这些特性的散列结果就可以用于验证信息是否被修改。
单向散列函数一般用于产生消息摘要,密钥加密等,常见的有:
l MD5(Message Digest Algorithm 5):是RSA数据安全公司开发的一种单向散列算法,非可逆,相同的明文产生相同的密文。
l SHA(Secure Hash Algorithm):可以对任意长度的数据运算生成一个160位的数值;
SHA-1与MD5的比较
因为二者均由MD4导出,SHA-1和MD5彼此很相似。相应的,他们的强度和其他特性也是相似,但还有以下几点不同:
l 对强行供给的安全性:最显著和最重要的区别是SHA-1摘要比MD5摘要长32 位。使用强行技术,产生任何一个报文使其摘要等于给定报摘要的难度对MD5是2128数量级的操作,而对SHA-1则是2160数量级的操作。这样,SHA-1对强行攻击有更大的强度。
l 对密码分析的安全性:由于MD5的设计,易受密码分析的攻击,SHA-1显得不易受这样的攻击。
l 速度:在相同的硬件上,SHA-1的运行速度比MD5慢。
以上综述了两种加密方法的原理,总体来说主要有下面几个方面的不同:
l 在管理方面:公钥密码算法只需要较少的资源就可以实现目的,在密钥的分配上,两者之间相差一个指数级别(一个是n一个是n2)。所以私钥密码算法不适应广域网的使用,而且更重要的一点是它不支持数字签名。
l 在安全方面:由于公钥密码算法基于未解决的数学难题,在破解上几乎不可能。对于私钥密码算法,到了AES虽说从理论来说是不可能破解的,但从计算机的发展角度来看。公钥更具有优越性。
l 从速度上来看:AES的软件实现速度已经达到了每秒数兆或数十兆比特。是公钥的100倍,如果用硬件来实现的话这个比值将扩大到1000倍。
由于非对称加密算法的运行速度比对称加密算法的速度慢很多,当我们需要加密大量的数据时,建议采用对称加密算法,提高加解密速度。
对称加密算法不能实现签名,因此签名只能非对称算法。
由于对称加密算法的密钥管理是一个复杂的过程,密钥的管理直接决定着他的安全性,因此当数据量很小时,我们可以考虑采用非对称加密算法。
在实际的操作过程中,我们通常采用的方式是:采用非对称加密算法管理对称算法的密钥,然后用对称加密算法加密数据,这样我们就集成了两类加密算法的优点,既实现了加密速度快的优点,又实现了安全方便管理密钥的优点。
那采用多少位的密钥呢? RSA建议采用1024位的数字,ECC建议采用160位,AES采用128为即可。
保密通信:保密通信是密码学产生的动因。使用公私钥密码体制进行保密通信时,信息接收者只有知道对应的密钥才可以解密该信息。
数字签名:数字签名技术可以代替传统的手写签名,而且从安全的角度考虑,数字签名具有很好的防伪造功能。在政府机关、军事领域、商业领域有广泛的应用环境。
秘密共享:秘密共享技术是指将一个秘密信息利用密码技术分拆成n个称为共享因子的信息,分发给n个成员,只有k(k≤n)个合法成员的共享因子才可以恢复该秘密信息,其中任何一个或m(m≤k)个成员合作都不知道该秘密信息。利用秘密共享技术可以控制任何需要多个人共同控制的秘密信息、命令等。
认证功能:在公开的信道上进行敏感信息的传输,采用签名技术实现对消息的真实性、完整性进行验证,通过验证公钥证书实现对通信主体的身份验证。
密钥管理:密钥是保密系统中更为脆弱而重要的环节,公钥密码体制是解决密钥管理工作的有力工具;利用公钥密码体制进行密钥协商和产生,保密通信双方不需要事先共享秘密信息;利用公钥密码体制进行密钥分发、保护、密钥托管、密钥恢复等。
基于公钥密码体制可以实现以上通用功能以外,还可以设计实现以下的系统:安全电子商务系统、电子现金系统、电子选举系统、电子招投标系统、电子彩票系统等。
深入浅出PageRank算法
PageRank算法是谷歌曾经独步天下的“倚天剑”,该算法由Larry Page和Sergey Brin在斯坦福大学读研时发明的,论文点击下载: The PageRank Citation Ranking: Bringing Order to the Web。
本文首先通过一些参考文献引出问题,然后给出了PageRank的几种实现算法,最后将其推广至在MapReduce框架下如何实现PageRank算法。
PageRank的核心思想有2点:
1.如果一个网页被很多其他网页链接到的话说明这个网页比较重要,也就是pagerank值会相对较高;
2.如果一个pagerank值很高的网页链接到一个其他的网页,那么被链接到的网页的pagerank值会相应地因此而提高。
下面是一张来自WikiPedia的图,每个球代表一个网页,球的大小反应了网页的pagerank值的大小。指向网页B和网页E的链接很多,所以B和E的pagerank值较高,另外,虽然很少有网页指向C,但是最重要的网页B指向了C,所以C的pagerank值比E还要大。

参考内容:
2.Google 的秘密- PageRank 彻底解说 中文版
3.数值分析与算法 Page 161 应用实例:Google的PageRank算法
4.Numeric Methods with Matlab 或者中文翻译版本Matlab数值计算
5.使用 MapReduce 思想计算 PageRank Page 62 PageRank和马尔可夫链
1.问题背景
来自参考内容3

2.数学建模
来自参考内容3,理解网页连接矩阵$G$,马尔科夫过程("网上冲浪"),转移矩阵$A$,概率$p$为用户点击当前网页中的某个链接地址的概率(一般都为0.85)。


最后得到一个等式$Ax=x$,这实际上就是求矩阵$A$的特征值为1的特征向量!
下面的内容使用圆盘定理解释了1是矩阵$A$的主特征值,所以我们可以使用幂法来求解。
关于幂法的详细介绍参考另一篇文章Numerical Methods Using Matlab: 第三章 矩阵特征值和奇异值求解


3.求解PageRank
假设有如上图右侧所示的网页链接模型。
(1) 幂法
wiki上有一个PageRank的简便算法,它不考虑转移概率,而是采用的是迭代的方式,每次都更新所有网页的pagerank值,更新的方式就是将每个网页的pagerank值平摊分给它指向的所有网页,每个网页累计所有指向它的网页平摊给它的值作为它该回合的pagerank值,直到全部网页的pagerank值收敛了或者满足一定的阈值条件就停止。
后面的MapReduce框架下PageRank算法的实现就采用了这个思想。考虑转移概率的情况和这个算法类似,乘上一个转移概率再加上一个随机跳转的概率。

根据上面的思想,下面Matlab代码实现可以得到各个网页的PageRank值。
n=6;
i=[2 3 4 4 5 6 1 6 1];
j=[1 2 2 3 3 3 4 5 6];
G=sparse(i,j,1,n,n);
% Power method
for j = 1:n
L{j} = find(G(:,j));
c(j) = length(L{j});
end
p = .85;
delta = (1-p)/n;
x = ones(n,1)/n;
z = zeros(n,1);
cnt = 0;
while max(abs(x-z)) > .0001
z = x;
x = zeros(n,1);
for j = 1:n
if c(j) == 0
x = x + z(j)/n;%转移到任意一个网页
else
x(L{j}) = x(L{j}) + z(j)/c(j);%将上次的pagerank值平摊给所有指向的网页
end
end
x = p*x + delta;
cnt = cnt+1;
end
得到的向量$x$保存了各个网页的pagerank值,虽然链接数目一样,但是网页①比网页④和网页⑤都高,而网页②的pagerank值第二高,因为网页①链接到了它上面,相当于沾了网页①的光。
x =
0.2675
0.2524
0.1323
0.1698
0.0625
0.1156
这篇文章给出该算法的一个Python版本实现,该博主使用第三方模块python-graph,python-graph模块实现了很多图算法,该模块的使用示例,使用前需要先安装,代码如下:
easy_install python-graph-core
easy_install python-graph-dot
Python版本的算法实现:
# coding=utf-8
# python-graph https://code.google.com/p/python-graph/
# Import graphviz
import graphviz as gv
# Import pygraph
from pygraph.classes.digraph import digraph
from pygraph.readwrite.dot import write
# Define pagerank function
def pagerank(graph, damping_factor=0.85, max_iterations=100, \
min_delta=0.00001):
"""
Compute and return the PageRank in an directed graph.
@type graph: digraph
@param graph: Digraph.
@type damping_factor: number
@param damping_factor: PageRank dumping factor.
@type max_iterations: number
@param max_iterations: Maximum number of iterations.
@type min_delta: number
@param min_delta: Smallest variation required for a new iteration.
@rtype: Dict
@return: Dict containing all the nodes PageRank.
"""
nodes = graph.nodes()
graph_size = len(nodes)
if graph_size == 0:
return {}
# value for nodes without inbound links
min_value = (1.0-damping_factor)/graph_size
# itialize the page rank dict with 1/N for all nodes
#pagerank = dict.fromkeys(nodes, 1.0/graph_size)
pagerank = dict.fromkeys(nodes, 1.0)
for i in range(max_iterations):
diff = 0 #total difference compared to last iteraction
# computes each node PageRank based on inbound links
for node in nodes:
rank = min_value
for referring_page in graph.incidents(node):
rank += damping_factor * pagerank[referring_page] / \
len(graph.neighbors(referring_page))
diff += abs(pagerank[node] - rank)
pagerank[node] = rank
print 'This is NO.%s iteration' % (i+1)
print pagerank
print ''
#stop if PageRank has converged
if diff < min_delta:
break
return pagerank
# Graph creation
gr = digraph()
# Add nodes and edges
gr.add_nodes(["1","2","3","4"])
gr.add_edge(("1","2"))
gr.add_edge(("1","3"))
gr.add_edge(("1","4"))
gr.add_edge(("2","3"))
gr.add_edge(("2","4"))
gr.add_edge(("3","4"))
gr.add_edge(("4","2"))
# Draw as PNG
# dot = write(gr)
# gvv = gv.readstring(dot)
# gv.layout(gvv,'dot')
# gv.render(gvv,'png','Model.png')
pagerank(gr)
经过32次迭代之后得到的结果如下,和前面的结果一致:
This is NO.32 iteration
{'1': 0.2675338708706491, '3': 0.13227261904986046, '2': 0.2524037902400518, '5': 0.062477242064127136, '4': 0.1697488529161491, '6': 0.1155828978186352}
(2) 利用马尔可夫矩阵的特殊结构
来自参考内容4,其中$\delta=\frac{1-p}{n}$

也就是将矩阵$A$进行分解,并不需要显示求出矩阵$A$,然后便是求解一个线性方程组即可。
function x = pagerank1(G)
% PAGERANK1 Google's PageRank modified version 1 - hujiawei
%if nargin < 3, p = .85; end
p=0.85;
% Eliminate any self-referential links
G = G - diag(diag(G));
% c = out-degree, r = in-degree
[n,n] = size(G);
c = sum(G,1);%each row's sum
r = sum(G,2);%each col's sum
% Scale column sums to be 1 (or 0 where there are no out links).
k = find(c~=0);
D = sparse(k,k,1./c(k),n,n);
% Solve (I - p*G*D)*x = e
e = ones(n,1);
I = speye(n,n);
x = (I - p*G*D)\e;
% Normalize so that sum(x) == 1.
x = x/sum(x);
(3) 巧妙解法:逆迭代算法
巧妙利用Matlab中的精度误差导致原本是一个奇异矩阵的$I-A$变成一个非奇异矩阵,运行时只是会有些警告提示,但是运行结果和其他算法一样。

function x = pagerank2(G)
% PAGERANK1 Google's PageRank modified version 2 - hujiawei
% using inverse iteration method
%if nargin < 3, p = .85; end
p=0.85;
% Eliminate any self-referential links
G = G - diag(diag(G));
% c = out-degree, r = in-degree
[n,n] = size(G);
c = sum(G,1);%each row's sum
r = sum(G,2);%each col's sum
% Scale column sums to be 1 (or 0 where there are no out links).
k = find(c~=0);
D = sparse(k,k,1./c(k),n,n);
% Solve (I - p*G*D)*x = e
e = ones(n,1);
I = speye(n,n);
% x = (I - p*G*D)\e;
delta=(1-p)/n;
A=p*G*D+delta;
x=(I-A)\e;
% Normalize so that sum(x) == 1.
x = x/sum(x);
最后,附上参考内容4中给出的一份好代码,用于模拟随机冲浪生成矩阵$G$的代码
function [U,G] = surfer(root,n)
% SURFER Create the adjacency graph of a portion of the Web.
% [U,G] = surfer(root,n) starts at the URL root and follows
% Web links until it forms an adjacency graph with n nodes.
% U = a cell array of n strings, the URLs of the nodes.
% G = an n-by-n sparse matrix with G(i,j)=1 if node j is linked to node i.
%
% Example: [U,G] = surfer('http://www.harvard.edu',500);
% See also PAGERANK.
%
% This function currently has two defects. (1) The algorithm for
% finding links is naive. We just look for the string 'http:'.
% (2) An attempt to read from a URL that is accessible, but very slow,
% might take an unacceptably long time to complete. In some cases,
% it may be necessary to have the operating system terminate MATLAB.
% Key words from such URLs can be added to the skip list in surfer.m.
% Initialize
clf
shg
set(gcf,'doublebuffer','on')
axis([0 n 0 n])
axis square
axis ij
box on
set(gca,'position',[.12 .20 .78 .78])
uicontrol('style','frame','units','normal','position',[.01 .09 .98 .07]);
uicontrol('style','frame','units','normal','position',[.01 .01 .98 .07]);
t1 = uicontrol('style','text','units','normal','position',[.02 .10 .94 .04], ...
'horiz','left');
t2 = uicontrol('style','text','units','normal','position',[.02 .02 .94 .04], ...
'horiz','left');
slow = uicontrol('style','toggle','units','normal', ...
'position',[.01 .24 .07 .05],'string','slow','value',0);
quit = uicontrol('style','toggle','units','normal', ...
'position',[.01 .17 .07 .05],'string','quit','value',0);
U = cell(n,1);
hash = zeros(n,1);
G = logical(sparse(n,n));
m = 1;
U{m} = root;
hash(m) = hashfun(root);
j = 1;
while j < n & get(quit,'value') == 0
% Try to open a page.
try
set(t1,'string',sprintf('%5d %s',j,U{j}))
set(t2,'string','');
drawnow
page = urlread(U{j});
catch
set(t1,'string',sprintf('fail: %5d %s',j,U{j}))
drawnow
continue
end
if get(slow,'value')
pause(.25)
end
% Follow the links from the open page.
for f = findstr('http:',page);
% A link starts with 'http:' and ends with the next quote.
e = min([findstr('"',page(f:end)) findstr('''',page(f:end))]);
if isempty(e), continue, end
url = deblank(page(f:f+e-2));
url(url<' ') = '!'; % Nonprintable characters
if url(end) == '/', url(end) = []; end
% Look for links that should be skipped.
skips = {'.gif','.jpg','.pdf','.css','lmscadsi','cybernet', ...
'search.cgi','.ram','www.w3.org', ...
'scripts','netscape','shockwave','webex','fansonly'};
skip = any(url=='!') | any(url=='?');
k = 0;
while ~skip & (k < length(skips))
k = k+1;
skip = ~isempty(findstr(url,skips{k}));
end
if skip
if isempty(findstr(url,'.gif')) & isempty(findstr(url,'.jpg'))
set(t2,'string',sprintf('skip: %s',url))
drawnow
if get(slow,'value')
pause(.25)
end
end
continue
end
% Check if page is already in url list.
i = 0;
for k = find(hash(1:m) == hashfun(url))';
if isequal(U{k},url)
i = k;
break
end
end
% Add a new url to the graph there if are fewer than n.
if (i == 0) & (m < n)
m = m+1;
U{m} = url;
hash(m) = hashfun(url);
i = m;
end
% Add a new link.
if i > 0
G(i,j) = 1;
set(t2,'string',sprintf('%5d %s',i,url))
line(j,i,'marker','.','markersize',6)
drawnow
if get(slow,'value')
pause(.25)
end
end
end
j = j+1;
end
delete(t1)
delete(t2)
delete(slow)
set(quit,'string','close','callback','close(gcf)','value',0)
%------------------------
function h = hashfun(url)
% Almost unique numeric hash code for pages already visited.
h = length(url) + 1024*sum(url);
4.MapReduce框架下PageRank算法的实现
利用前面wiki上的迭代(或者幂法)的思想来实现MapReduce框架下PageRank算法很简单,可以先阅读下参考内容5。
这篇文章using-mapreduce-to-compute-pagerank更加详细,可以参考
以下是我的大数据的一次作业,要求是参考wiki上的简便算法,实现MapReduce框架下的PageRank算法。给的数据集是Twitter的用户之间的关系,可以看做是网页之间的关系,但是助教没要求写代码以及运行这个数据集(有1G多),所以下面只是一个Python版本的理想可行版本,并没有通过实际大数据集的验证,另外,博主暂时还不太会Python的mapreduce框架中的一些函数,所以实现的是一个简明的可以测试的PageRank算法。
1.输入输出格式
map函数的输入是<节点,从该节点引出的边列表>,其中节点是一个类,包含了其当前的pagerank值,输出是<节点,反向节点pagerank值/反向节点引出边的总数>;
reduce函数的输入是<节点,反向节点pagerank值/反向节点引出边的总数>,输出是<节点,从该节点引出的边列表>,其中节点包含了其更新后的pagerank值。
伪代码: [一时犯二写了个英文形式的 ]
process the data to the form of {node i:[its adjacent node list],...}
while the sum of difference between the last two pagerank values < threshold
map({node i:[its adjacent node list],...}):
map_output={}
for every node j in adjacent node list:
put or sum up {j:(i, PageRank(i)/length(adjacent node list))} into map_output
return map_output
reduce(map_output):
reduce_output={}
for every entry {j:(i, PageRank(i)/length(adjacent node list))} in map_output:
put or sum up all values pagerank values for node j with its adjacent node list into reduce_output
return reduce_output
2.示例演示
假设用户1,2,3,4是如下图所示的关系:

假设有2个mapper(A和B)和1个reducer(C),初始时4个节点的pagerank值都是0.25
其中,关于用户1和2的数据被mapperA读取并处理,关于用户3和4的数据被mapperB读取并处理 [经验证,即使一个用户的数据是由不同的mapper来读取的,最终收敛到的结果差不多]
map的输入输出结果如下:

reduce的输入输出结果如下,输入是2个mapper的输出,输出的结果中更新了节点的pagerank值

reducer处理完了之后又将它的结果输入给mapper处理,直到迭代的次数超过了设定值或者两次迭代之后得到的所有节点的pagerank值之差的总和(也可以是取二范数)小于设定的阈值。
3.示例的实验结果
(1)首先是使用Matlab采用幂法的方式计算出在p=1.0的情况下示例得到的结果 [它的主要作用是验证后面python版本的正确性]
matlab源码如下:
n=4;
i=[2 3 4 3 4 4 1 2];
j=[1 1 1 2 2 3 3 4];
G=sparse(i,j,1,n,n);
[n,n] = size(G);
for j = 1:n
L{j} = find(G(:,j));
c(j) = length(L{j});
end
% Power method
p=1.0;
delta = (1-p)/n;
x = ones(n,1)/n;
z = zeros(n,1);
cnt = 0;
while max(abs(x-z)) > .0001
z = x;
x = zeros(n,1);
for j = 1:n
if c(j) == 0
x = x + z(j)/n;
else
x(L{j}) = x(L{j}) + z(j)/c(j);
end
end
x = p*x + delta;
cnt = cnt+1;
end
sprintf('pagerank result:')
x
结果为:
0.1072
0.3571
0.2143
0.3214
(2)matlab版本的page rank没有采用mapreduce的思想进行迭代,所以我另外写了一个python版本的利用mapreduce思想实现的pagerank算法(注:我并没有使用python的map和reduce函数去实现,而是使用更加容易明白的实现),使用的阈值为0.0001,最多迭代的次数为100次。
# coding=utf-8
__author__ = 'hujiawei'
__doc__ = 'pagerank mapreduce'
class Node:
def __init__(self,id,pk):
self.id=id
self.pk=pk
def pk_map(map_input):
map_output={}
for node,outlinks in map_input.items():
for link in outlinks:
size=len(outlinks)
if link in map_output:
map_output[link]+=(float)(node.pk)/size
else:
map_output[link]=(float)(node.pk)/size
return map_output
def pk_reduce(reduce_input):
for result in reduce_input:
for node,value in result.items():
node.pk+=value
def pk_clear(nodes):
for node in nodes:
node.pk=0
def pk_last(nodes):
lastnodes=[]
for node in nodes:
lastnodes.append(Node(node.id,node.pk))
return lastnodes
def pk_diff(nodes,lastnodes):
diff=0
for i in range(len(nodes)):
print('node pk %f, last node pk %f ' % (nodes[i].pk, lastnodes[i].pk))
diff+=abs(nodes[i].pk-lastnodes[i].pk)
return diff
def pk_test1():
node1 = Node(1, 0.25)
node2 = Node(2, 0.25)
node3 = Node(3, 0.25)
node4 = Node(4, 0.25)
nodes = [node1, node2, node3, node4]
threshold = 0.0001
max_iters = 100
for iter_count in range(max_iters):
iter_count += 1
lastnodes=pk_last(nodes)
print('============ map count %d =================' % (iter_count))
in1 = {node1: [node2, node3, node4], node2: [node3, node4]}
in2 = {node3: [node1, node4], node4: [node2]}
mapout1 = pk_map(in1)
mapout2 = pk_map(in2)
for node, value in mapout1.items():
print str(node.id) + ' ' + str(value)
for node, value in mapout2.items():
print str(node.id) + ' ' + str(value)
print('============ reduce count %d =================' % (iter_count))
reducein = [mapout1, mapout2]
pk_clear(nodes)
pk_reduce(reducein)
for node in nodes:
print str(node.id) + ' ' + str(node.pk)
diff=pk_diff(nodes,lastnodes)
if diff < threshold:
break
if __name__ == '__main__':
pk_test1()
得到的结果为如下,总共迭代了15次
1 0.107138774577
2 0.35712924859
3 0.214296601128
4 0.321435375705
上面的结果和Matlab用幂法得到的pagerank值差别很小,可以认为是正确的,所以说明了使用这种mapreduce输入输出格式的正确性。
OK,差不多了,希望对需要理解PageRank算法的人有帮助! 🙂
常用排序算法的动画效果图
http://www.atool.org/sort.php
1 快速排序
介绍:
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来,且在大部分真实世界的数据,可以决定设计的选择,减少所需时间的二次方项之可能性。
步骤:
- 从数列中挑出一个元素,称为 "基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
排序效果:

详细过程:
2 归并排序
介绍:
归并排序(Merge sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用
步骤:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
排序效果:

详细过程:
3 堆排序
介绍:
堆积排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
步骤:
(比较复杂,自己上网查吧)
排序效果:

详细过程:
(暂无)
4 选择排序
介绍:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此类推,直到所有元素均排序完毕。
排序效果:

详细过程:
5 冒泡排序
介绍:
冒泡排序(Bubble Sort,台湾译为:泡沫排序或气泡排序)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
步骤:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
排序效果:

详细过程:
6 插入排序
介绍:
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置中
- 重复步骤2
排序效果:
(暂无)
详细过程:
7 希尔排序
介绍:
希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
- 但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
排序效果:

北京市小汽车摇号程序的反编译、算法及存在的问题浅析-不重复随机数列生成算法
给定一个正整数n,需要输出一个长度为n的数组,数组元素是随机数,范围为0 – n-1,且元素不能重复。比如 n = 3 时,需要获取一个长度为3的数组,元素范围为0-2,
比如 0,2,1。
这个问题的通常解决方案就是设计一个 hashtable ,然后循环获取随机数,再到 hashtable 中找,如果hashtable 中没有这个数,则输出。下面给出这种算法的代码
public static int[] GetRandomSequence0(int total)
{
int[] hashtable = new int[total];
int[] output = new int[total];
Random random = new Random();
for (int i = 0; i < total; i++)
{
int num = random.Next(0, total);
while (hashtable[num] > 0)
{
num = random.Next(0, total);
}
output[i] = num;
hashtable[num] = 1;
}
return output;
}
代码很简单,从 0 到 total - 1 循环获取随机数,再去hashtable 中尝试匹配,如果这个数在hashtable中不存在,则输出,并把这个数在hashtable 中置1,否则循环尝试获取随机数,直到找到一个不在hashtable 中的数为止。这个算法的问题在于需要不断尝试获取随机数,在hashtable 接近满时,这个尝试失败的概率会越来越高。
那么有没有什么算法,不需要这样反复尝试吗?答案是肯定的。
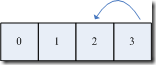
如上图所示,我们设计一个顺序的数组,假设n = 4
第一轮,我们取 0 – 3 之间的随机数,假设为2,这时,我们把数组位置为2的数取出来输出,并把这个数从数组中删除,这时这个数组变成了
第二轮,我们再取 0-2 之间的随机数,假设为1,并把这个位置的数输出,同时把这个数从数组删除,以此类推,直到这个数组的长度为0。这时我们就可以得到一个随机的不重复的序列。
这个算法的好处是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试。算法代码如下:
public static int[] GetRandomSequence1(int total)
{
List<int> input = new List<int>();
for (int i = 0; i < total; i++)
{
input.Add(i);
}
List<int> output = new List<int>();
Random random = new Random();
int end = total;
for (int i = 0; i < total; i++)
{
int num = random.Next(0, end);
output.Add(input[num]);
input.RemoveAt(num);
end--;
}
return output.ToArray();
}
这个算法把两个循环改成了一个循环,算法复杂度大大降低了,按说速度应该比第一个算法要快才对,然而现实往往超出我们的想象,当total = 100000 时,测试下来,第一个算法用时 44ms, 第二个用时 1038 ms ,慢了很多!这是为什么呢?问题的关键就在这个 input.RemoveAt 上了,我们知道如果要删除一个数组元素,我们需要把这个数组元素后面的所有元素都向前移动1,这个移动操作是非常耗时的,这个算法慢就慢在这里。到这里,可能有人要说了,那我们不用数组,用链表,那删除不就很快了吗?没错,链表是能解决删除元素的效率问题,但查找的速度又大大降低了,无法像数组那样根据数组元素下标直接定位到元素。所以用链表也是不行的。到这里似乎我们已经走到了死胡同,难道我们只能用hashtable 反复尝试来做吗?在看下面内容之前,请各位读者先思考5分钟。
…… 思考5分钟
算法就像一层窗户纸,隔着窗户纸,你永远无法知道里面是什么,一旦捅穿,又觉得非常简单。这个算法对于我,只用了2分钟时间想出来,因为我经常实现算法,脑子里有一些模式,如果你的大脑还没有完成这种经验的积累,也许你要花比我长很多的时间来考虑这个问题,也许永远也找不到捅穿它的方法。不过不要紧,我把这个方法公布出来,有了这个方法,你只需轻轻一动,一个完全不同的世界便出现在你的眼前。原来就这么简单……。
还是上面那个例子,假设 n = 4
第一轮,我们随机获得2时,我们不将 2 从数组中移除,而是将数组的最后一个元素移动到2的位置
这时数组变成了
第二轮我们对 0-2 取随机数,这时数组可用的最后一个元素位置已经变成了2,而不是3。假设这时取到随机数为1
我们再把下标为2 的元素移动到下标1,这时数组变成了
以此类推,直到取出n个元素为止。
这个算法的优点是不需要用一个hashtable 来存储已获取的数字,不需要反复尝试,也不用像上一个算法那样删除数组元素,要做的只是每次把数组有效位置的最后一个元素移动到当前位置就可以了,这样算法的复杂度就降低为 O(n) ,速度大大提高。
经测试,在 n= 100000 时,这个算法的用时仅为7ms。
下面给出这个算法的实现代码
/// <summary>
/// Designed by eaglet
/// </summary>
/// <param name="total"></param>
/// <returns></returns>
public static int[] GetRandomSequence2(int total)
{
int[] sequence = new int[total];
int[] output = new int[total];
for (int i = 0; i < total; i++)
{
sequence[i] = i;
}
Random random = new Random();
int end = total - 1;
for (int i = 0; i < total; i++)
{
int num = random.Next(0, end + 1);
output[i] = sequence[num];
sequence[num] = sequence[end];
end--;
}
return output;
}
下面是n 等于1万,10万和100万时的测试数据,时间单位为毫秒。从测试数据看GetRandomSequence2的用时和n基本成正比,线性增长的,这个和理论上的算法复杂度O(n)也是一致的,另外两个算法则随着n的增大,用时超过了线性增长。在1百万时,我的算法比用hashtable的算法要快10倍以上。
| 10000 | 100000 | 1000000 | |
| GetRandomSequence0 | 5 | 44 | 1075 |
| GetRandomSequence1 | 11 | 1038 | 124205 |
| GetRandomSequence2 | 1 | 7 | 82 |
现在摇号的程序及数据都可以在官网中查看,目的就是通过信息的透明度来堵住那些说摇号系统有猫腻之类的传言,我做为一个程序员,下意识的就想看看到底是否有猫腻。
通过下载程序,导入数据,将种子数写入后,的确没有什么猫腻,但还是不死心,想研究一下算法,结果发现了惊人的事情。
此算法使用的是伪随机,简单点将就是当种子数一定,摇号数据一定,每次随机结果都是一样的。举个例子,借用某申请编码2245102443992,摇号基数序号500015,取种子数范围在100000至120000之间能中签的种子数,结果显示共132个种子数,其概率为0.66%。随机找了一个种子数100575进行计算,得出结果在左侧表中,查询2245102443992是否中签,结果显示中签,在第15916行摇中;所以大家都应该知道怎么回事了吧,只要摇号池数据确定,查询出摇号基数序号,就能算出中签的种子数都有哪些,所以公布的数据和程序又有何用?关键在于种子数的确定。